Surprises !
En parcourant des sites de maths et de physique (on est geek ou on ne l'est pas), j'ai fait ma récolte de vérités contre-intuitives ou surprenantes que je vous propose de découvrir dans ce billet.
Rassurez-vous, je vous épargnerai le paradoxe des anniversaires.
L'incommensurable hasard des cartes
Prenez un jeu de 52 cartes et mélangez-le bien. D'après vous, depuis l'invention du jeu de 52 cartes, combien de fois ce mélange précis a-t-il déjà été obtenu ?
La réponse est : probablement jamais. En effet, il y a de l'ordre de 10 puissance 68 mélanges possibles pour un jeu de 52 cartes (un 1 suivi de 68 zéros), ce qui est environ le nombre d'atomes dans notre galaxie.
Et si vous prenez un jeu de tarot de 78 cartes, le nombre de mélanges possibles dépasse largement le nombre d'atomes dans l'univers observable. C'est-à-dire que pour l'obtenir, vous prenez le nombre d'atomes dans l'univers observable et vous ajoutez encore 35 zéros derrière.
Un cadeau vraiment unique ? Offrez un paquet de cartes mélangé !
L'épi inévitable
Si ce n'était pour sa curieuse conséquence pratique, ce résultat mathématique mériterait d'être évoqué rien que pour son nom : il s'agit du théorème de la boule chevelue.
Il dit (entre autres) qu'on ne peut pas plaquer des cheveux sur une boule sans créer au moins un épi, une raie ou une zone sans cheveux.
Mais cela s'applique-t-il à la tête humaine qui n'est chevelue que sur le dessus ? Eh bien, étant donné que l'implantation de nos cheveux est orientée vers la périphérie, oui. Nous sommes condamnés à l'épi.
Une autre conséquence est qu'il y a toujours au moins un point de la planète où existe un courant cyclonique (vent orienté vers le bas ou vers le haut, mais sans déplacement d'air horizontal).
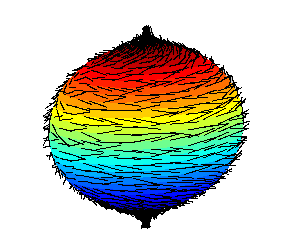 Impossible de lisser des vecteurs tangents à une boule : des discontinuités apparaissent toujours.
Impossible de lisser des vecteurs tangents à une boule : des discontinuités apparaissent toujours.
Point fixe
Du théorème de la boule chevelue, on en déduit un autre au nom moins funky, le théorème du point fixe de Brouwer.
La conséquence qu'on aime souvent citer est la suivante : entre le moment où on commence à touiller son café et le moment où on a fini de le touiller, il y a au moins une molécule du liquide qui est revenue à sa position initiale. Et si on re-touille pour la faire dégager, alors c'est une autre qui revient à sa position initiale. Ça me semble foireux pour deux raisons : 1) je ne mets pas de sucre dans mon café et 2) ça ne fonctionne que si le touillage impose au café une déformation continue, or je soupçonne qu'un touillage énergique ne soit pas si continu que ça (deux molécules qui étaient voisines peuvent se retrouver arbitrairement loin l'une de l'autre à l'issue du touillage, dirais-je intuitivement).
Par contre, une expérience tout aussi simple a une conséquence tout aussi frappante : prenez deux feuilles de papier. Froissez-en une (aussi violemment que vous le voulez, du moment qu'elle n'est pas déchirée) puis aplatissez-la sur l'autre (avec un fer à repasser ou ce que vous voulez). Vous pouvez alors être sûr et certain qu'un point de la feuille froissée se situe exactement au-dessus de son homologue de la feuille intacte. Quant à dire lequel, ce n'est pas forcément évident…
La terre tourne aussi autour de la lune
Un peu de physique pour changer.
Ce qui suit va à l'encontre de tout ce qu'on apprend à l'école, et pourtant, c'est la vérité. La lune ne tourne pas autour de la terre. En effet, la terre attire la lune, mais la lune attire aussi un peu la terre. Donc la terre tourne aussi un peu autour de la lune. En fait, l'ensemble terre-lune tourne autour de son centre de masse qui se trouve à 4600 km du centre de la terre (c'est-à-dire 1700 km sous vos pieds quand vous avez la lune au-dessus de la tête).
On peut suivre le même raisonnement pour l'ensemble terre-soleil, mais le soleil est tellement massif que le centre de masse de l'ensemble n'est qu'à quelques centaines de kilomètres du centre du soleil.
Poids
Votre poids durant la journée est supérieur à votre poids durant la nuit. Si vous pesez 80 kg, cet écart peut aller jusqu'à 100 grammes selon votre position sur la planète. La rotation de la terre autour du soleil produit un effet de centrifugeuse qui vous alourdit le jour et vous allège la nuit.
Quant à la rotation de la terre sur elle-même, elle vous allège de 275 grammes si vous vous trouvez à l'équateur.
En revanche, la rotation de l'ensemble terre-lune autour de son centre de masse (voir ci-dessus) modifie votre poids de moins de 0,25 gramme.
Bref, si vous voulez mettre toutes les chances de votre côté lors d'un prochain régime, allez à l'équateur et attendez une nuit de nouvelle lune pour vous peser.
Orbite lunaire
Quand on imagine la trajectoire de la lune vue du soleil, on pense à quelque chose comme ça, une espèce de cordon de téléphone qui représente la rotation de la lune enroulée autour de l'orbite terrestre :

En fait, la terre avance beaucoup trop vite pour que la lune ait le temps de refermer ses boucles. À ce stade, vous imaginez peut-être un cordon de téléphone très étiré et une trajectoire qui est simplement sinueuse, comme ça :

En réalité, ça peut paraître contre-intuitif, mais la trajectoire de la lune vue du soleil est entièrement concave, c'est-à-dire que malgré son mouvement de rotation autour de la terre qui la fait s'éloigner du soleil la moitié du temps, la lune ne cesse jamais de tomber vers le soleil. Comment peut-elle tomber vers le soleil tout en s'en éloignant ?
Il faut expliquer ce qu'on entend par « tomber vers ». Un satellite tombe constamment vers l'objet autour duquel il orbite. C'est juste qu'il va assez vite pour tomber toujours derrière l'horizon et en faire perpétuellement le tour sans jamais s'y écraser. Les fusées qui lancent les satellites artificiels sont là pour les élever dans l'espace mais aussi pour leur donner cette énorme vitesse horizontale qui leur permet de tomber vers la terre… sans s'en rapprocher. Par tomber, on entend donc « se rapprocher du sol qu'on a sous les pieds, s'il était plat ». Mais malgré tous les efforts et les bûchers déployés pour nous persuader du contraire, on croit désormais savoir que les corps célestes sont à peu près sphériques. Le sol plat vers lequel on tombe est donc une pure vue de l'esprit et — ouf — on ne s'y écrase pas.
La lune, donc, ne cesse jamais d'avoir une trajectoire recourbée vers le soleil, et pourtant elle s'en éloigne la moitié du temps.
Et voici à quoi ça ressemble (j'ai exagéré l'orbite de la lune pour mettre en évidence la forme un peu anguleuse… car en réalité, à l'œil nu, l'orbite réelle est impossible à distinguer d'un cercle) :

(J'en profite pour signaler que les courbes ont été réalisées avec l'excellent Desmos que j'ai découvert pour l'occasion.)
Largeur constante et trous carrés
En parlant de choses rondes…
Si vous êtes déjà allé outre-Manche, peut-être avez vous remarqué que la pièce de 50 pence n'est pas ronde mais comporte des faces légèrement arrondies :
 (Elle a pas l'air commode, la reine…)
(Elle a pas l'air commode, la reine…)
Ces arrondis ne sont pas un caprice du designer, ils sont une nécessité technique pour que les distributeurs et autres automates à pièces puissent mesurer la largeur de la pièce quelle qu'en soit l'orientation. Car cette pièce est une forme de largeur constante (c'est-à-dire que si on la fait rouler entre deux règles parallèles, l'espacement des règles ne varie pas).
Contrairement à ce que nous dit l'intuition, le cercle n'est pas la seule forme ayant la même largeur quelle que soit son orientation. Il y en a une infinité.
Et on peut même s'en servir pour inventer une perceuse qui fait des trous carrés.
Hauteur et altitude
L'Everest est la plus haute montagne. Est-ce que ça signifie que le sommet de l'Everest est le plus éloigné du centre de la terre ?
Non ! C'est le Chimborazo, en Équateur.
Là, vous vous précipitez sur Wikipédia pour constater que son altitude n'est que de 6268 m, alors que l'Everest culmine à 8848 m. Où est l'astuce ?
L'altitude est mesurée par rapport au niveau de la mer (c'est-à-dire au niveau qu'aurait la mer si elle s'étendait jusque là) mais la terre n'est pas sphérique. Entre le Chimborazo et l'Everest, le niveau de la mer varie de plus de 4 km par rapport au centre de la terre !
Premier chiffre
Prenez un nombre au hasard, non pas dans votre tête, mais dans votre environnement : poids inscrit sur une boîte de conserve, prix d'un article, taille d'un fichier…
La loi de Benford dit quelle est la probabilité que le premier chiffre soit un 1, un 2, un 3, etc. Le premier chiffre ne pouvant pas être un zéro, on aurait tendance à dire que chacun des chiffres restants a une chance sur neuf d'être observé.
En réalité, la probabilité d'observer un 1 est d'environ 30%, avec des probabilités décroissantes pour les chiffres suivants :
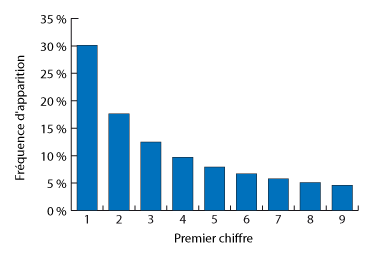
Explication : les nombres qu'on rencontre au quotidien ont tous ce qu'on pourrait appeler un maximum approximatif qui dépend de leur type. Or, quand on compte de zéro à ce maximum, pour la plupart des maximums, le premier chiffre sera plus souvent un 1 qu'un 9. Par exemple, si je prends au hasard une page d'un livre qui en compte 500, j'ai 111 chances sur 500, donc 22,2% de chances que son numéro commence par 1 (la page 1, les 10 pages de 10 à 19 et les 100 pages de 100 à 199). Ainsi, le chiffre 1 sera toujours sur-représenté. Il n'y a que si mon livre compte 99 pages, ou 999 pages, que le premier chiffre sera un 1 avec une probabilité d'1/9. L'astuce pour établir la loi de Benford est de dire que les maximums des valeurs suivent eux-mêmes la loi de Benford, ainsi que leurs maximums, et les maximums des maximums des maximums, etc., à l'infini.
Outre le côté amusant, cette loi a des applications très pratiques. On s'en sert notamment pour repérer des données falsifiées (comptabilité remaniée, fraude électorale…). Le cerveau humain n'est pas très bon pour imaginer des valeurs réparties « comme des vraies ».
Doh !
Changeons de sujet et parlons statistiques…
Le paradoxe de Simpson invite à se méfier des raisonnements vite faits et des intuitions. Cet article du British Medical Journal rapporte un cas réel assez troublant.
Une étude a comparé le taux de succès de deux traitements des calculs rénaux. Chaque traitement a été testé sur 350 patients. Le traitement A a eu un taux de succès de 78% et le traitement B a eu un taux de succès de 83%.
L'étude s'est ensuite intéressée à la taille des calculs traités. Pour les calculs de moins de 2 cm, le traitement A était plus efficace que le B (93% de succès contre 83%), inversant en cela le résultat global.
C'est donc, se dit-on, que le traitement B se rattrape en étant très efficace sur les calculs de plus de 2 cm. Et là, en vérifiant les taux de succès, surprise : sur les calculs de plus de 2 cm, le traitement A a aussi été plus efficace que le B (73% contre 69%).
Pour résumer :
- sur l'ensemble des calculs traités, B est plus efficace que A ;
- sur les petits calculs, A est plus efficace que B ;
- sur les gros calculs, A est plus efficace que B.
Comme ça m'énervait de ne pas comprendre ce qui se passait, j'ai décidé de faire un dessin avec les données réelles :
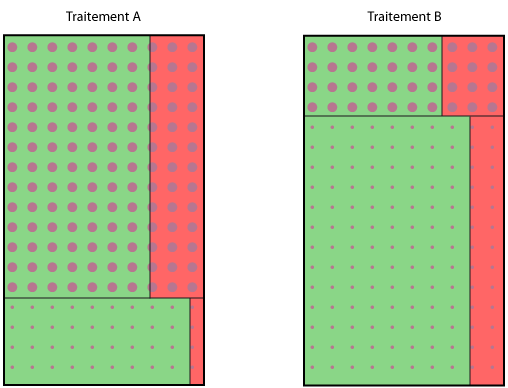
Les petits pois correspondent aux petits calculs, les gros pois aux gros calculs. En vert, les patients traités avec succès.
Là, le problème saute aux yeux : pour les deux traitements, les petits calculs sont bien plus faciles à traiter. Le traitement A est clairement meilleur que le B dans tous les cas, mais l'étude B a eu affaire à beaucoup de patients souffrant de petits calculs, donc faciles à traiter. Et même s'ils ont été moins bien traités que par le traitement A, ils étaient si nombreux qu'ils ont fait pencher la balance globale en faveur de B. S'il y a bien un point sur lequel la deuxième étude (B) a été meilleure, c'est pour sélectionner des patients moins malades.
Ça laisse pensif sur tout un tas de choses… Les classements des meilleurs lycées (taux de réussite global ou par filière ? avec ou sans sélection à l'entrée ? si c'est un taux d'acceptation en études supérieures, est-ce que les écoles visées étaient faciles à atteindre ? etc.), des meilleurs hôpitaux…
Bouchons
Un autre résultat totalement contre-intuitif est le paradoxe de Braess. Une de ses conséquences est que parfois (et même assez souvent), ajouter une route de forte capacité à un réseau routier peut faire empirer la durée de trajet de tout le monde.
En gros, on arrive dans une situation où l'automobiliste a le choix entre deux routes de départ pour entrer sur le réseau routier : par la route A, selon le trafic, le trajet met entre 1h30 et 2h. Par la route B, quel que soit le trafic, le trajet met 2h. La route A étant au pire pareille que la route B, et parfois meilleure, tout le monde prend la route A. Donc tout le monde met deux heures. Bien sûr, ce ne serait pas se sacrifier de prendre la route B pour fluidifier le trafic de l'autre côté, puisqu'on ne mettrait pas plus de temps. Mais personne ne le fait car tout le monde a envie que ce soient les autres qui se sacrifient.
Cette situation n'est pas directement le paradoxe de Braess mais le paradoxe de Braess dit que la construction d'une nouvelle route peut faire basculer un réseau routier d'un équilibre où le trafic se répartit équitablement entre deux routes équivalentes (où tout le monde met 1h30) à la situation décrite ci-dessus où le temps de circulation augmente quand les automobilistes cherchent à le réduire (et finalement tout le monde met 2h).
Ce n'est pas qu'un cas théorique : il a déjà été observé que la fermeture d'une route de forte capacité améliorait le trafic.
Pouet
Pour finir, prenez une trompette ayant ce profil :
 (Il s'agit de la courbe y=1/x et ce qu'on obtient en lui faisant faire un tour complet s'appelle une trompette de Gabriel.)
(Il s'agit de la courbe y=1/x et ce qu'on obtient en lui faisant faire un tour complet s'appelle une trompette de Gabriel.)
Il faut imaginer qu'elle est infiniment longue et que son diamètre devient infiniment petit.
On calcule assez facilement que la surface de la trompette est d'aire infinie. S'il vous prenait l'envie de la peindre, vous n'en finiriez jamais.
En revanche, si vous n'avez que ça sous la main pour stocker votre peinture, sachez que vous pouvez remplir la trompette avec à peine plus de 3 litres avant qu'elle ne déborde (π litres, exactement).
Voilà une forme d'aire infinie et de volume fini.
Mais où est l'astuce, avec la peinture ? Après tout, si je veux peindre l'intérieur, je n'ai qu'à le remplir. Entre une quantité infinie de peinture et 3 litres, je fais une économie substantielle.
L'astuce est que la peinture a toujours une épaisseur, donc un volume, et qu'on ne peut plus parler en termes d'aire. Il est donc vrai qu'il me faudrait une quantité infinie de peinture pour peindre l'extérieur de ma trompette au pinceau. Il est vrai aussi qu'il me suffirait de 3,14 litres pour la remplir. Ce qui est faux, c'est de dire que la remplir permettrait d'en peindre tout l'intérieur. Au bout d'un moment, le conduit deviendrait trop fin et plus rien ne coulerait. Il faudrait pour cela une peinture aux molécules infiniment petites, c'est-à-dire pas de peinture, ou de la peinture imaginaire. Et c'est là, avec de la peinture imaginaire, qu'on a un joli paradoxe.
23 avril 2014
Commentaires
Une surprise de taille en effet: un nouveau billet !
Ça fait plaisir à lire. Le coup de la perceuse à trous carrés... génial !
En ce qui concerne le trafic, je connaissais aussi un autre paradoxe: les bouchons peuvent se créer à l'endroit où la vitesse des automobilistes augmente. Par exemple un premier tronçon à 50 puis un deuxième à 70 a des risques de créer un bouchon à la frontière des 2 tronçons. L'explication tient dans le fait que le tronçon à 50 a un débit plus grand que celui du tronçon à 70 car les voitures sont plus espacées.
Merci et continue !
23 avril 2014